В 2002 году она выиграла миллион долларов в лотерее Cool Million, имея
шансы 1:5200000. А четыре года спустя, приняв участие в лотерее Jubilee,
стала обладательницей второго миллиона. На этот раз шансы на выигрыш
оценивались как 1:7 056 00. Каков же был ее шанс выиграть главный приз в
обеих лотереях? Его нетрудно подсчитать: 1 :(5200 000x705 600) = 1:3
669 120 000 000, или примерно один из 3,7 триллиона. Шанс и в самом деле
ничтожно мал, в чем можно убедиться, если представить себе другую
лотерею.

Допустим, что в ней участвуют все жители Земли — 7 млрд.
человек. Выпущенные по такому случаю 3,7 триллиона билетов со стираемым
защитным слоем, из которых лишь один выигрышный, распределены между
ними поровну. По правилам лотереи в регулярном еженедельном розыгрыше
каждый участник использует один билет. Конечно, первый же открытый билет
может оказаться выигравшим. Однако в самом неблагоприятном случае
ожидание выпадения счастливого билета растянется на 10 лет!

Надо
сказать, в истории американских лотерей (коих множество, и проводятся
они постоянно) было всего несколько случаев с повторным выигрышем
призов, превышающих миллион долларов. Правда, все они касались обычных
лотерей, в которых джекпот, как правило, куда больше главного приза в
мгновенной лотерее. Примечательно также, что один из самых крупных
выигрышей — 254 млн. долларов — достался в 2007 году 84-летнему
пенсионеру, чья фамилия оказалась... Вильсон. Вот и не верь после этого в совпадения.

А рекордсменкой по количеству крупных выигрышей стала Джоан Гинтер
из Лас-Вегаса. За 17 лет она побеждала в различных лотереях четыре раза
— последний в 2010 году — и «заработала» таким образом более 20 млн.
долларов. Согласно расчетам, учтя имевшиеся каждый раз шансы выиграть,
подобное достижение возможно лишь в одном случае из 36 х 1024, или 36
септиллионов, на фоне которых меркнут даже 3,7 триллиона, или 3,7 х
10¹²!

Как остроумно и верно заметил по этому поводу один
американский профессор математики, специалист в области теории
вероятностей, случай сей поразительный, однако у вероятности нет памяти!
И что характерно, шансы Джоан выиграть в очередной лотерее точно такие
же, как и у любого другого игрока. Иными словами, они есть всегда, пусть
и крошечные. Должно быть, перед покупкой очередного билета подобные
мысли посещают (более того — обнадеживают) многих любителей лотерей.

Заветная шестерка

«Случилось
невероятное!» — так прокомментировал директор болгарской лотереи «6 из
42» выпадение в двух тиражах подряд одинаковых выигрышных чисел: 4, 15,
23, 24, 35 и 42. Произошли эти события в сентябре 2009 года, с разницей
всего в четыре дня. В простое совпадение никто, включая очевидцев, тогда
не поверил. Однако тщательная проверка, проведенная под личным
контролем министра спорта, в чьем ведении находится лотерея, фактов
махинаций не выявила. Почему же все усомнились в том, что одна и та же
выигрышная комбинация чисел выпала два раза подряд случайно?

Сделаем
простой расчет. Всего способов выбрать шесть из сорока двух различных
чисел имеется Значит, вероятность выпадения единственно возможного
выигрышного набора чисел в любом тираже равна


А
серьезные сомнения в случайности выпадения одной и той же числовой
комбинации в двух тиражах подряд возникли из-за того, что вероятность
этого события крайне мала, всего


Заметим,
что в подобных лотереях повторное выпадение выигрышного набора чисел
изредка все же происходит (в той же Болгарии такое было два-три раза),
правда, не в двух тиражах кряду. А вот интересно, что предприняли бы
организаторы лотереи, если бы числа выпали дважды, да еще в одном и том
же порядке?

Между тем если в первый раз шесть чисел не угадал
никто, то во второй на них поставили сразу 18 человек! Надежды тех, кто
рассчитывал на крупный выигрыш, не оправдались: призовую сумму пришлось
делить на всех. Словно желая опровергнуть законы теории вероятностей,
накануне следующего тиража многие всерьез обсуждали, не поставить ли на
те же числа снова, ведь не исключено, что они выпадут и в третий раз!

Если
одни игроки в лотерею рассчитывают победить благодаря якобы придуманной
ими системе угадывания чисел (рано или поздно она, возможно, и даст
результат — по законам все той же теории вероятностей), то другие
придерживаются примитивных стратегий. Ставишь, например, всегда на один и
тот же набор чисел и ждешь, когда он выпадет (если вообще выпадет).
Поступавшему так американцу Крису Хоффману, любителю лотереи «5 из 39»,
можно сказать, крупно повезло: ждать пришлось всего-то 15 лет! О том,
сколько средств он потратил за это время на покупку билетов, а главное,
покрыл ли все расходы выигрыш в размере 150 тысяч долларов, история
умалчивает.

«Бесплатная» лотерея

Кстати, о
потраченных деньгах. В середине 1990-х в США проводилась «почтовая
лотерея». В ней разыгрывался денежный приз в 5 млн. долларов, а шанс
получить его составлял 1 из 200 млн. От участников требовалось всего
ничего: сделать ставку и отправить ее по почте. Разрешалось делать
сколько угодно ставок, но с условием — высылать их по одной. Стоит ли
участвовать в такой «бесплатной» лотерее?

При таких условиях,
конечно, не стоит. И вот почему. Зная вероятность выигрыша и его сумму,
легко подсчитать ожидаемый выигрыш игрока*:


Однако
расходы на отправку письма куда больше! Иначе говоря, ожидаемый выигрыш
во много раз меньше вложенной игроком суммы, и их разность выражается
числом отрицательным. Так что если тратиться на пересылку многократно,
очень скоро придется подсчитывать убытки.

Как тут не вспомнить
рассказ Антона Павловича Чехова «Житейские невзгоды»? Если бы его герой
сразу прикинул, во сколько ему обойдется покупка выигрышного билета
внутреннего займа, участвовавшего в денежной лотерее, то всерьез
призадумался, нужен ли он ему вообще.

Кому же выгодна «почтовая
лотерея»? Ответ очевиден: почтовой службе США. По самым скромным
подсчетам, при благоприятном развитии событий доход с отправленных писем
должен был превзойти заявленный приз как минимум в десять раз.

Народные лотереи

Существуют
лотереи с вещевыми призами. Недаром их часто называют «народными». Вот
лишь один из примеров. Чего только не придумывают транспортники, чтобы
заставить пассажиров платить за проезд! Весной 2010 года в Барнауле
(Россия) проводилась стимулирующая лотерея «Счастливый билет». В ней
разыгрывались номер и серия разовых проездных билетов на трамвай и
троллейбус. Призы выдавались «натурой»: подарочными картами гипермаркета
электроники, месячными проездными на городской транспорт и тому
подобным. Стоит ли говорить, что за три недели проведения лотереи число
«зайцев» резко сократилось, а доходы транспортников (при скромных в
общем-то затратах) ощутимо возросли!


Бывает,
сам процесс игры захватывает не меньше, чем желание получить приз,
особенно когда возможность выигрыша заложена в каждый билет. Об этом
заявляют, например, организаторы моментальной «Всероссийской жилищной
лотереи». А дальше, как и положено в рекламе: «Не верите? Не хотите
рисковать? Все еще сомневаетесь? Тогда мы идем к вам!» И не просто так, а
с разумным предложением потренироваться для начала на виртуальных
лотерейных билетах.

Правила игры просты. В билете девять строк
(этажей), по два игровых окна в каждой; в одном из них спрятано
«счастливое число», равное сумме выигрыша (она указана на защитном
слое). Задача проста — угадать это число, открыв только одно окно в
строке. Таким образом, двигаясь построчно снизу вверх, можно по желанию
открыть от одного до девяти окон. При первой же неудаче игра
прекращается, билет считается невыигрышным. Так насколько справедливо
заявление организаторов? Ясно, что вероятность выбора «счастливого
числа» на каждом шаге одна и та же — она равна одной второй — и по ходу
игры убывает в геометрической прогрессии:

А какова средняя сумма выигрыша, приходящаяся на один билет? Если сделать всего один шаг из девяти, то она составит


и
далее будет только уменьшаться (из-за того, что вероятность выигрыша
убывает значительно быстрее, нежели растет призовая сумма), а проигрыш,
напротив, будет увеличиваться.

Сколько ни тренируйся, а
предугадать исход игры в каждом конкретном случае невозможно. А вот
сесть за компьютер все же стоит. Если достаточно долго
экспериментировать с виртуальными билетами и фиксировать результаты,
можно заметить, как проявит себя «закон больших чисел» — с увеличением
числа испытаний частота появления события (выпадения крупного денежного
приза) приближается к его вероятности, а последняя, как мы убедились,
невелика.

Имея билет на руках, благоразумно ограничиться
угадыванием чисел во второй-третьей строках и скромным выигрышем.
Очевидно, так же рассудили многие участники лотереи. А на что всегда
рассчитывают ее устроители? Как и в любой азартной игре — на
человеческие слабости и неумение вовремя остановиться. Поэтому уже на
билетах следующей партии «по многочисленным просьбам игроков» была
выделена строка с несгораемой суммой (на седьмом этаже), а также
добавилось новое правило: если на пятой или шестой строке окажется
открытым окно с символом «+», игра закончится, а вы получите
утешительный приз — 50 рублей. Устроителям лотереи в изобретательности
не откажешь, не так ли? Как думаете, стали ли правила честнее и возросла
ли после этих нововведений продажа билетов?

Непростительный промах

Допускают
ли организаторы лотерей просчеты? Не поверите, но и такое случается.
Следующая история произошла в одном американском штате 20 лет назад.
Карточки очередного тиража лотереи «6 из 44» продавались по 1 доллару, в
то время как призовой фонд составлял на тот момент 27,9 млн. долларов, и
почти все они приходились на джекпот.

Несколько инвесторов
сообразили, что смогут хорошо заработать, выкупив и заполнив карточки
всеми возможными комбинациями шести из сорока четырех чисел. Они учли
дополнительные расходы и риски (в частности, изучив статистику
предыдущих розыгрышей, выяснили: в 120 случаях победителей не оказалось,
в 40 был один победитель, еще в 10 — два) и заодно оценили прибыль. Для
осуществления задуманного привлекли 2,5 тысячи мелких инвесторов из
разных стран, а также группу людей для работы с карточками. В итоге
из-за нехватки времени удалось использовать всего 70% карточек от
запланированного числа, но и этого хватило, чтобы выиграть главный приз.
А ведь повезло!

В чем заключался финансовый просчет
организаторов лотереи, побудивший инвесторов пойти на сговор? И каковы
были, по их подсчетам, общий ожидаемый выигрыш и прибыль с одного
вложенного доллара? (Второстепенными расходами можно пренебречь.)
Просчет был в том, что организаторы лотереи продавали лотерейные
карточки по невыгодной для себя цене. На самом деле ее следовало
увеличить в четыре раза. Действительно, для гарантированной победы нужно
заполнить


карточек.
Призовой фонд — 27,9 млн. долларов. Значит, карточка должна стоить хотя
бы 27900000 : 7059052 = 3,95 доллара**. Неудивительно, что цена 1
доллар показалась инвесторам очень привлекательной. В идеале доход с нее
составляет 2,95 доллара. Как показывают расчеты, общий ожидаемый
выигрыш равен


Даже с учетом всех затрат доход оказался бы огромным!

Нетрудно
догадаться, чем закончилась эта история. Узнав, что главный приз
достался группе инвесторов, устроители лотереи поначалу не хотели
выплачивать выигрыш. Но после непродолжительных юридических пререканий
были вынуждены признать, что причин для отказа нет. В итоге им пришлось
дорого заплатить за собственный промах. Случай исключительный и довольно
поучительный.

Доводы рассудка

Так стоит ли
участвовать в лотереях в надежде быстро разбогатеть? Стоит ли полагаться
на случай в погоне за легкими деньгами? Повезет или нет — большой
вопрос. В лотереи регулярно играют миллионы людей по всему миру, а
побеждают единицы. Но в одном можно не сомневаться — в любой лотерее
всегда выигрывают организаторы.

Никаких надежных стратегий
угадывания чисел в лото или выявления счастливого билета в мгновенной
лотерее не существует, кроме как заполнить все карточки или скупить все
билеты. Но это возможно лишь при условии, что игроки объединят усилия, и
имеет смысл делать, только если призовой фонд значительно превышает
стоимость всех билетов, на что рассчитывать не приходится.

В
лотерее типа «почтовой» устроители и игроки решают две обратные задачи:
первые подбирают комбинацию, которую не угадает никто, а вторые ее
старательно отгадывают, — и наблюдать за этим «состязанием» все же
интереснее, чем за случайным выпадением чисел в лото. Каковы шансы на
успех у тех и других в теории? А на практике? Как ни странно, разные: не
секрет, что никак не связанные между собой участники нередко ставят на
одни и те же комбинации, а любого рода совпадения и повторы на руку
организаторам: почти всегда можно просчитать наиболее вероятный «круг»
таких комбинаций.

Устроители лотереи заинтересованы в том, чтобы в
ней участвовало как можно больше народа. При подходящем ожидаемом
выигрыше и приемлемой цене на билеты любой призовой фонд быстро окупится
за счет проданного количества билетов (о том, какая их доля приходится
на тот или иной выигрыш, игрокам, конечно, неведомо). На продажу влияют и
размер приза, и вероятность выигрыша, а ее можно варьировать, изменяя
правила игры. Так, если эта вероятность довольно велика (а в таком
случае выигрыш всегда маловат) или, напротив, слишком мала, продажа
лотерейных билетов падает. Одним словом, успех лотереи во многом зависит
от умения устроителей отыскать ту «золотую середину» между величиной
призов и шансом выиграть, которая обеспечила бы им крупный доход. И этим
искусством они прекрасно владеют, будучи знакомы и с психологией
любителей азартных игр, и с основами теории вероятностей.

И,
наконец, главный довод рассудка, не только подтвержденный многовековым
опытом, но и научно обоснованный: во всякой азартной игре каждый раз все
решают везение и случай, но чем больше играешь, тем больше
проигрываешь.

Словарик к статье

Сочетание —
выборка к элементов из п имеющихся (к меньше, или равно п), при которой
их порядок неважен. Число всевозможных сочетаний из п элементов по к
обозначается и вычисляется по формуле


Случайное событие — событие (результат, исход испытания), которое объективно может произойти или не произойти в данном испытании.

Вероятность события А
— число, выражающее меру объективной возможности наступления случайного
события А; определяется как отношение числа m исходов испытания,
благоприятствующих этому событию (влекущих за собой его наступление), к
числу п всех равновозможных исходов, то есть равно


Случайная величина — переменная величина X, которая может принимать то или иное значение в зависимости от случая.

Математическое ожидание
(или среднее значение) случайной величины X, принимающей конечное число
значений x1. х2.....хп, — число, равное сумме произведений этих
значений на соответствующие им вероятности р1. р2.....рп,  то есть

 







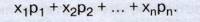Комментарии к статье

*
Средняя сумма выигрыша, которая приходится на один билет. Определяется
как сумма произведений возможных выигрышей на вероятности их выпадения.

**
Минимальная цена лотерейного билета равна математическому ожиданию
выигрыша игрока. В данном примере «мелкие» выигрыши, по сути не влияющие
на результат, в расчет не принимались.

Н. Карпушина
"Открытия и гипотезы" №8 2012